Binary Tree
In Data Structure, the simplest form of the tree is Binary Tree. Each node of binary tree can have a maximum of two children. They are called Left Subtree and Right Subtree.
Binary Tree Components
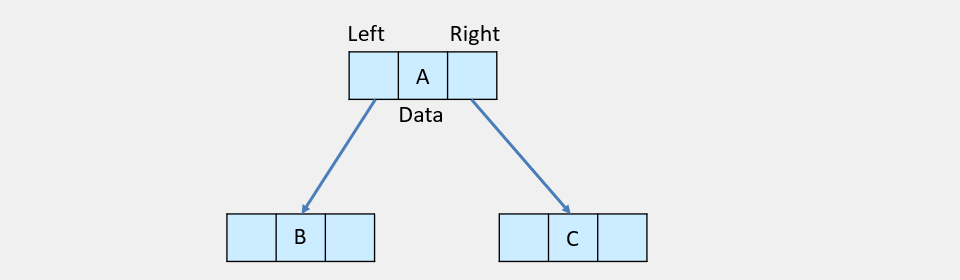
Each node of Binary tree has three components-
- Pointer for Left Subtree
- Pointer for Right Subtree
- Data Element
Types of Binary Tree
- Strictly Binary Tree
- Complete Binary Tree
- Extended Binary Tree
Strictly Binary Tree
In the strictly binary tree, every node of the tree contains non empty left subtree and non empty right subtree.
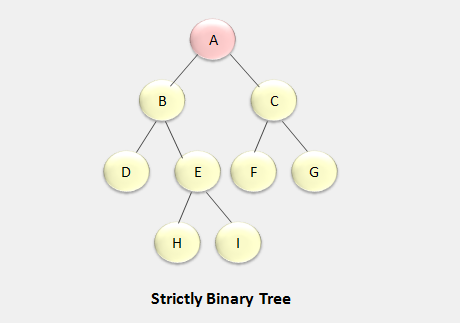
In the above binary tree, all the non terminal nodes having non empty left and right sub trees. Such as B and C has non empty left and right subtrees.
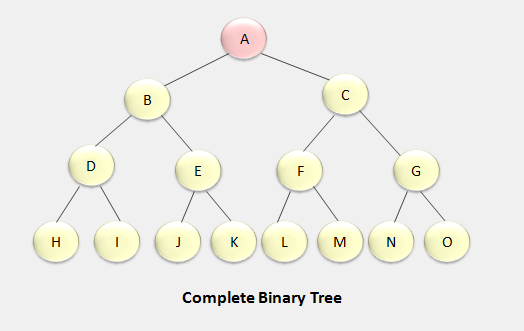
Complete Binary Tree
A complete binary has one node at level 0, two nodes at level 1, four nodes at level 2 and so on. If l is the level, then each level contains 2l nodes, like 3rd level contain 23 = 8 levels.
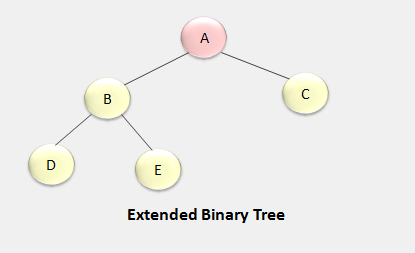
Extended Binary Tree
In the extended binary tree, each node has either 0 or 2 children. The node with two children are called internal nodes and the node with 0 children are called external nodes. The extended binary tree is also called 2-tree.
Binary Tree Program in C
#include<stdio.h>
#include<
struct node
{
int data;
struct node *rnode;
struct node *lnode;
}*tmp=NULL;
typedef struct node NODE;
NODE *create_binarytree();
void preorder_traversal(NODE *);
void inorder_traversal(NODE *);
void postorder_traversal(NODE *);
void insert_element(NODE *);
int main()
{
int n,i,choice;
do
{
printf("\nEnter 1 to create binary tree");
printf("\nEnter 2 to insert element in tree");
printf("\nEnter 3 to preorder traversal");
printf("\nEnter 4 to postorder traversal");
printf("\nEnter 5 to inorder traversal");
printf("\nEnter 6 to exit");
printf("\nEnter Your Choice : ");
scanf("%d",&choice);
switch(choice)
{
case 1:
tmp=create_binarytree();
break;
case 2:
insert_element(tmp);
break;
case 3:
printf("\n\nPreorder Traversal of Binary Tree : ");
preorder_traversal(tmp);
break;
case 4:
printf("\n\nPostorder Traversal of Binary Tree : ");
postorder_traversal(tmp);
break;
case 5:
printf("\n\nInorder Traversal of Binary Tree : ");
inorder_traversal(tmp);
break;
case 6:
exit(0);
default:
printf("\n Please Enter Valid Choice");
}
}
while(n!=5);
}
void insert_element(NODE *root)
{
NODE *newnode;
if(root==NULL)
{
newnode=create_binarytree();
root=newnode;
}
else
{
newnode=create_binarytree();
while(1)
{
if(newnode->datadata)
{
if(root->lnode==NULL)
{
root->lnode=newnode;
break;
}
root=root->lnode;
}
if(newnode->data>root->data)
{
if(root->rnode==NULL)
{
root->rnode=newnode;
break;
}
root=root->rnode;
}
}
}
}
NODE *create_binarytree()
{
NODE *newnode;
int n;
newnode=(NODE *)malloc(sizeof(NODE));
printf("\n\nEnter the Data ");
scanf("%d",&n);
newnode->data=n;
newnode->lnode=NULL;
newnode->rnode=NULL;
return(newnode);
}
void postorder_traversal(NODE *tmp)
{
if(tmp!=NULL)
{
postorder_traversal(tmp->lnode);
postorder_traversal(tmp->rnode);
printf("%d->",tmp->data);
}
}
void inorder_traversal(NODE *tmp)
{
if(tmp!=NULL)
{
inorder_traversal(tmp->lnode);
printf("%d->",tmp->data);
inorder_traversal(tmp->rnode);
}
}
void preorder_traversal(NODE *tmp)
{
if(tmp!=NULL)
{
printf("%d->",tmp->data);
preorder_traversal(tmp->lnode);
preorder_traversal(tmp->rnode);
}
}
Output of the above program-
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 1
Enter the Data 47
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 2
Enter the Data 90
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 2
Enter the Data 43
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 2
Enter the Data 89
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 2
Enter the Data 34
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 3
Preorder Traversal of Binary Tree : 47->43->34->90->89->
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 4
Postorder Traversal of Binary Tree : 34->43->89->90->47->
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 5
Inorder Traversal of Binary Tree : 34->43->47->89->90->
Enter 1 to create binary tree
Enter 2 to insert element in tree
Enter 3 to preorder traversal
Enter 4 to postorder traversal
Enter 5 to inorder traversal
Enter 6 to exit
Enter Your Choice : 













