Binary Tree Traversal

There are different technique for tree traversal.

Pre-order Traversal
Post-order Traversal
In-order Traversal

Pre-order Traversal

The Pre-order Traversal follows this process-

It first process the root node, then traverse the left subtree in pre-order, then traverse the right subtree in pre-order.
If there are no any left or right children of node or node is empty, then the traversal is nothing performed.

Pre-order Traversal Algorithm

Suppose there is a binary tree, whose root node is given by pointer T. The Pre-order traversal process is given below.

STEP 1: [Check for empty tree]
IF T = NULL
Then print('Tree is empty')
	return
else print(DATA(T))
STEP 2: [Process the left subtree]
IF LPTR(T) != NULL
Then PPREORDER(LPTR(T))
STEP 3: [Process the right subtree] 
IF RPTR(T) != NULL
Then PPREORDER(RPTR(T))
STEP 4: Exit

Pre-order Traversal Example

Suppose, we have the following binary tree.

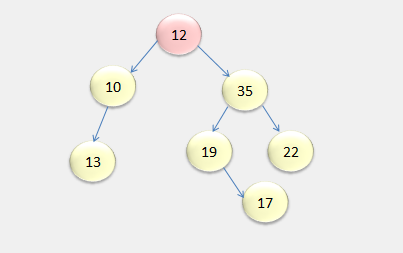
Pre-order Traversal : 12, 10, 13, 35, 19, 17, 22

Post-order Traversal

The Post-order Traversal follows this process-

It first traverse the left subtree in post-order, then traverse the right subtree in post-order, then process the root node, .

Post-order Traversal Algorithm

Suppose there is a binary tree, whose root node is given by pointer T. The Post-order traversal process is given below.

STEP 1: [Check for empty tree]
IF T = NULL
Then print('Tree is empty')
	return
else print(DATA(T))
STEP 2: [Process the left subtree]
IF LPTR(T) != NULL
Then PPOSTORDER(LPTR(T))
STEP 3: [Process the right subtree] 
IF RPTR(T) != NULL
Then PPREORDER(RPTR(T))
STEP 4: [Process the root node] 
print(DATA(T))
STEP 5: Exit

Post-order Traversal Example

Suppose, we have the following binary tree.

Post-order Traversal : 13, 10, 17, 19, 22, 35, 12

In-order Traversal

The In-order Traversal follows these process-

It first traverse the left subtree in in-order, then process the root node, then traverse the right subtree in in-order.

In-order Traversal Algorithm

Suppose there is a binary tree, whose root node is given by pointer T. The In-order traversal process is given below.

STEP 1: [Check for empty tree]
IF T = NULL
Then print('Tree is empty')
	return
else print(DATA(T))
STEP 2: [Process the left subtree]
IF LPTR(T) != NULL
Then RINORDER(LPTR(T))
STEP 3: [Process the root node] 
print(DATA(T))
STEP 4: [Process the right subtree] 
IF RPTR(T) != NULL
Then PPREORDER(RPTR(T))
STEP 5: Exit