Cicular Queue

In Circular queue, elements in a queue are arranged in a circular way. In this front and rear ends are joined together, which solves the dequeue re buffering problem and prevents excessive use of memory. It also follows the FIFO principle.

Suppose we have a linear queue. Now if we want to insert in the queue, then it is not possible because the queue is completely full. Now delete the two successors from the queue, but the overflow condition still exists because REAR = MAX - 1. This is the major drawback of a linear queue. This can be fixed if we shift the elements to the left, but this can be a time-consuming process.

As you can also see through this image. The queue is full and we can insert any element.

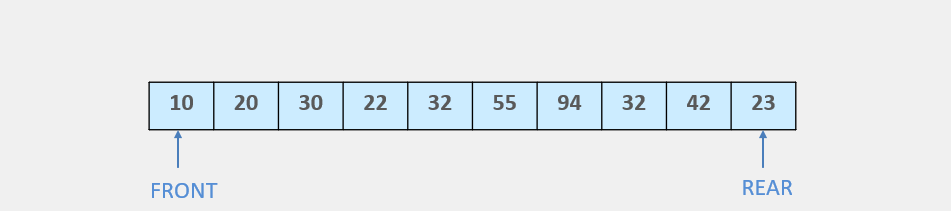
Here, we have deleted four elements from the queue. But we cannot insert any element because the REAR is still at the last position. This is the major problem in the queue. It has empty positions, but we cannot use them.

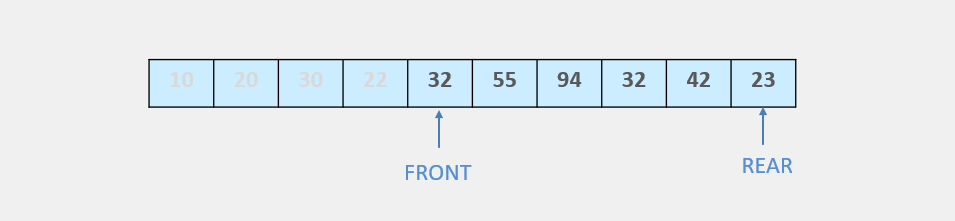
Circular Queue is introduced to fix this problem. The circular queue shows overloaded only when FRONT = 0 and REAR = MAX - 1.

Insertion in the Circular Queue

To insert values in a circular queue, we have to check the following conditions.

• If FRONT = 0 and REAR = MAX - 1 , then the circular queue is full.
• If REAR != MAX - 1, then REAR can be increased.
• If FRONT != 0 and REAR = MAX - 1, then it means queue is not full.

Algorithm to insert an element in a Circular queue

Step 1: IF FRONT = 0 and Rear = MAX - 1
Write OVERFLOW
Exit
Step 2: IF FRONT = -1 and REAR = -1
		SET FRONT = REAR = 0
	ELSE IF REAR = MAX - 1 and FRONT != 0
		SET REAR = 0
	ELSE
		SET REAR = REAR + 1
	[END OF IF]
Step 3: SET QUEUE[REAR] = VAL
Step 4: EXIT

Deletion in Circular Queue

To delete values in a circular queue, we have to check the following conditions.

• If FRONT = -1, then there is no element in the queue.
• If FRONT = REAR and the queue are not empty, then after deleting the element from the front, the queue becomes empty, so the FRONT and REAR are set to -1.
• If FRONT = MAX - 1, and the queue is not empty, then after deleting the element from the front the queue becomes empty.

Algorithm to delete element in a Circular queue

Step 1: IF FRONT = -1
Write UNDERFLOW
Goto Step 4
[END of IF]
Step 2: SET VAL = QUEUE[FRONT]
Step 3: IF FRONT = REAR
SET FRONT = REAR = -1
ELSE
IF FRONT = MAX -1
SET FRONT = 0
ELSE
SET FRONT = FRONT + 1
[END of IF]
Step 4: EXIT

Circular Queue Program in C

#include<stdio.h>
#define max 30
int q[10],front=0,rear=-1;
void main()
{
    int che;
    void insert_element();
    void delete_element();
    void display_element();
    printf("\nCircular Queue operations");
	printf("\n Enter 1 to insert into queue");
	printf("\n Enter 2 to delete element");
	printf("\n Enter 3 to display element");
	printf("\n Enter 4 to exit");

    do
	{
        printf("\n Enter your choice: ");
        scanf("%d",&che);
        switch(che)
        {
        case 1: insert_element();
            break;
        case 2: delete_element();
            break;
        case 3: display_element();
            break;
        case 4:
		exit(0);
            default:
            printf("Invalid input \n");
        }
    }while(1);
  return 0;
}
 
void insert_element()
{
    int x;
    if((front==0&&rear==max-1)||(front>0&&rear==front-1))
        printf("Circular Queue Overflow\n");
    else
    {
        printf("\n Enter a value to insert: ");
        scanf("%d",&x);
        if(rear==max-1&&front>0)
        {
            rear=0;
            q[rear]=x;
        }
        else
        {
            if((front==0&&rear==-1)||(rear!=front-1))
                q[++rear]=x;
        }
    }
}
void  delete_element()
{
    int a;
    if((front==0)&&(rear==-1))
    {
        printf("Circular Queue Underflow \n");
    }
    if(front==rear)
    {
        a=q[front];
        rear=-1;
        front=0;
    }
    else
        if(front==max-1)
        {
            a=q[front];
            front=0;
        }
        else a=q[front++];
        printf("\n Element deleted from the queue :%d\n",a);
}
 
void display_element()
{
    int i,j;
    if(front==0&&rear==-1)
    {
        printf("Circular Queue Underflow \n");
    }
    if(front>rear)
    {
        for(i=0;i<=rear;i++)
            printf("\t%d",q[i]);
        for(j=front;j<=max-1;j++)
            printf("\t%d",q[j]);
        printf("\nREAR: %d\n",q[rear]);
        printf("\nFRONT: %d\n",q[front]);
    }
    else
    {
        for(i=front;i<=rear;i++)
        {
            printf("\t%d",q[i]);
        }
        printf("\nREAR: %d\n",q[rear]);
        printf("\nFRONT: %d\n",q[front]);
    }
    printf("\n");
}

Output of the above program:

Circular Queue operations
 Enter 1 to insert into queue
 Enter 2 to delete element
 Enter 3 to display element
 Enter 4 to exit
 Enter your choice: 1

 Enter a value to insert: 10

 Enter your choice: 1

 Enter a value to insert: 39

 Enter your choice: 1

 Enter a value to insert: 89

 Enter your choice: 3
	10	39	89
 REAR: 89

 FRONT: 10


 Enter your choice: 2

 Element deleted from the queue :10

 Enter your choice: 3
	39	89
 REAR: 89

 FRONT: 39


 Enter your choice: